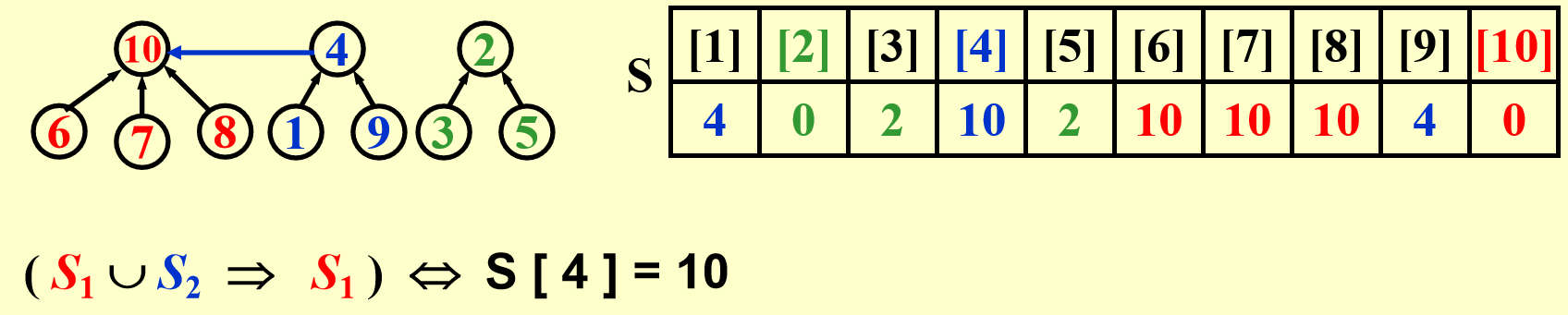Chap 8 The Disjoint Set ADT¶
约 1539 个字 100 行代码 预计阅读时间 9 分钟
核心知识
- 等价关系、等价类
- 核心操作
Union- Union by Size
- Union by Height
Find- 路径压缩
Equivalence Relations¶
定义:
- 集合 \(S\) 的关系(relation)\(R\),对于每对元素 \((a ,b), a, b \in S\),它们的关系 \(a \ R\ b\),如果其值为真,那么称 \(a\) 与 \(b\) 相关(\(a\) is related to \(b\))
-
对于集合 \(S\) 的一种关系 \(\sim\),如果它满足自反性(reflexive)、对称性(symmetric)和传递性(transitive),那么称这种关系为等价关系(equivalence relation)
- 自反性:\(\forall a \in S, a\ R\ a\)
- 对称性:\(a\ R\ b \leftrightarrow b\ R\ a\)
- 传递性:\((a\ R\ b) \wedge (b\ R\ c) \rightarrow a\ R\ c\)
-
对于元素 \(a \in S\) 的等价类(equivalence class),是包含所有与 \(a\) 相关的元素的 \(S\) 的子集
等价类相当于 \(S\) 内的分区(partition),\(S\)内的每个元素仅出现在一个等价类中
注:等价关系的详细知识参见离散数学Chap 9
The Dynamic Equivalence Problem¶
问题
给定等价关系 \(\sim\),对于任何的 \(a, b\),判断 \(a \sim b\) 是否成立
🌰
算法——并查集(Union/Find, the disjoint set),这是一种动态的(dynamic),在线(on-line)算法
动态:在算法执行过程中,
Union()会随时更新集合
伪代码模版:
Algorithm: (Union / Find)
{
// step 1: read the relations in
initialize N disjoint sets;
while (read in a~b)
{
if (!(Find(a) == Find(b)))
Union the two sets;
} // end-while
// step 2: decide if a~b
while (read in a and b)
if (Find(a) == Find(b))
output(true) ;
else
output(false);
}
-
集合的元素(elements):\(1, 2, 3, \dots, N\)
初始状态:有\(N\)个集合,每个集合仅有1个元素
-
对于一组集合 \(S_1, S_2, \dots \dots\),如果满足 \(S_i \cap S_j = \emptyset(i \ne j)\),称这些集合为不相交(disjoint)
如何在程序中表示这种数据结构?——树,并注意“指针”应从孩子节点指向父节点
-
运算(operations)
Union(i, j): 用 \(S = S_i \cup S_j\) 取代 \(S_i\) 和 \(S_j\)Find(i):找到包含元素 \(i\) 的集合 \(S_k\)
Basic Data Structure¶
// Declaration
#ifndef _DisjSet_H
typedef int DisjSet[NumSet + 1];
typedef int SetType;
typedef int ElementType;
void Initialize(DisjSet S);
void SetUnion(DisjSet S, SetType Root1, SetType Root2);
SetType Find(ElementType X, DisjSet S);
#endif // _DisjSet_H
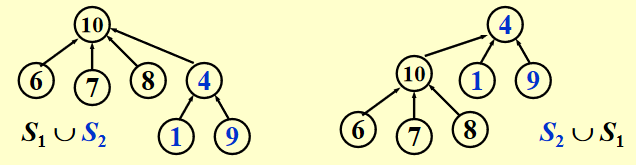
Union(i, j)¶
思路
令 \(S_i\) 为 \(S_j\) 的子树(反过来也行),也就是说,我们将其中一棵树的根节点指向另一棵树的根节点
实现方法
代码实现:
void Initialize(DisjSet S)
{
int i;
for (i = NumSets; i > 0; i--)
S[i] = 0;
}
void SetUnion(DisSet S, SetType Rt1, SetType Rt2)
{
S[Rt2] = Rt1;
}
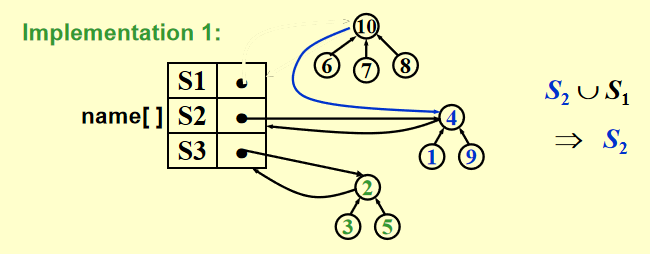
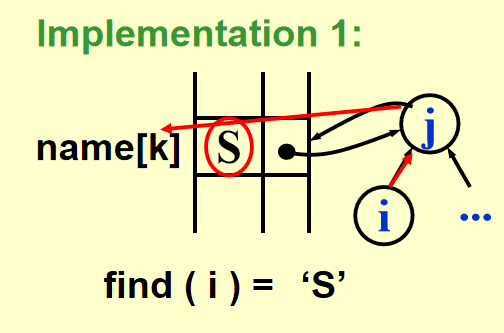
Find(i)¶
实现方法
Analysis¶
因为 union() 和 find() 操作往往是成对出现的,因此要分析该算法的复杂度,需要考虑执行一系列的 union() + find() 运算
代码实现完整的并查集操作:
// 使用上述算法实现的并查运算
{
Initialize S[i] = {i} for i = 1,..., 12;
for (k = 1; k <= Size; k++) // 对于每一对i~j
if (Find(i) != Find(j))
SetUnion(Find(i), Find(j));
}

Union() 函数前,一定要先调用 Find() 找到元素所在集合(树)的根节点,因为我们要合并 2 个完整的并查集,而不是 2 个节点。
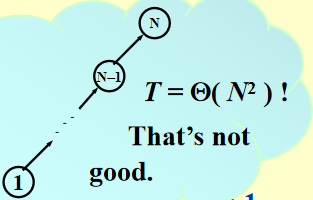
考虑最坏情况:union(2, 1), find(1); union(3, 2), find(2); ...... union(N, N - 1), find(1);,这些操作最终使一棵树退化成一个链表,此时时间复杂度为 \(\Theta(N^2)\)
Smart Union Algorithms¶
Union-by-Size¶
根据规模(size)合并树:总是将规模小的树合并到规模大的树上,令 S[Root] = -size,初始化为 -1
引理:令树 \(T\) 为通过 union-by-size 方法构造出的,且有 \(N\) 个节点,则:
证明:利用数学归纳法
因此 Find() 的时间复杂度变为 \(O(\log N)\)
整个算法的时间复杂度:\(O(N + M \log N)\)(进行 \(N\) 次合并操作和 \(M\) 次查找操作后)
代码实现:
void SetUnion(DisjSet S, SetType Root1, SetType Root2)
{
if (Root1 == Root2) // 如果是同一棵树,啥都不用做
return;
if (S[Root2] < S[Root1]) // 如果 Root2 对应树的规模更大
{
S[Root2] += S[Root1];
S[Root1] = Root2;
}
else // 如果 Root1 对应树的规模更大
{
S[Root1] += S[Root2];
S[Root2] = Root1;
}
}
Union-by-Height(rank)¶
根据高度(height)合并树:总是将矮的那棵树合并到高的那棵树上,因此每次 Union() 后树的高度最多增加1(当2棵树高度相同时)。令 S[Root] = -height,初始化为 -1
代码实现:
void SetUnion(DisjSet S, SetType Root1, SetType Root2)
{
if (S[Root2] < S[Root1])
S[Root1] = Root2;
else
{
if (S[Root1] == S[Root2])
S[Root1]--;
S[Root2] = Root1;
}
}
Path Compression¶
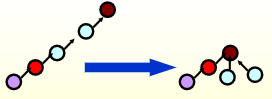
经过上述改进,Union 算法的性能已经不能再提升了,因此我们考虑改进 Find 算法。于是我们便用到了路径压缩(path compression)的方法——对于从根节点到 \(X\) 路径上的每个节点,将它的父节点设为根节点
示意图:
代码实现
// algorithm1--recursion
SetType Find(ElementType X, DisSet S)
{
if (S[X] <= 0)
return X;
else
// 让 X 的父节点为 X 原来父节点的父节点,这样的最终效果是:
// 从根节点到 X 的路径上,除根节点外的所有节点的父节点均为根节点,实现路径压缩
return S[X] = Find(S[X], S);
}
// algorithm2--iteration
SetType Find(ElementType X, DisSet S)
{
ElementType root, trail, lead; // trail 表示当前处理的节点,lead 表示下一个要处理的节点
for (root = X; S[root] > 0; root = S[root]); // find the root
for (trail = X; trail != root; trail = lead)
// 将路径上的所有节点的父节点都设为根节点
{
lead = S[trail];
S[trail] = root;
} // collapsing
return root
}
- 虽然这种算法相较于上一种,查找单个元素的速度变慢(因为多了一次赋值);但是对于查找整个序列的元素,这个算法的速度更快(因为多出来的赋值压缩了整棵树,对于频繁的合并操作显然是有利的)
- 该方法与 union-by-height 的方法不兼容,因为树的高度发生改变。所以推荐使用 union-by-size
Worst Case for Union-by-Rank and Path Compression¶
并查集的实现较为简单,但要分析它的时间复杂度相当困难。下面的内容仅供参考,考试不做要求。
引理:令 \(T(M, N)\) 为处理混合运算 \(M \ge N\) 查找运算和 \(N - 1\) 次合并运算的所需最大时间,那么对于正常数 \(k_1, k_2\): $$ k_1M \alpha(M, N) \le T(M, N) \le k_2M \alpha(M, N) $$ 即并查集最坏情况的时间复杂度为:\(\Theta(M\alpha (M, N))\)
阿克曼函数(Ackermann's Function):\(\alpha (M, N)\)
注:即使\(i, j\)数字很小,\(A(i, j)\)结果可能也非常大,比如\(A(2, 4) = 2^{65536}\)
\(\alpha (M, N) = \min\{ i\ge 1 | A(i, \lfloor M / N \rfloor )> \log N\} \le O(\log^* N) \le 4\)
其中 \(\log^*N\) 是阿克曼函数的反函数,代表用于 \(N\) 的对数的次数,使其最终结果 \(\le 1\)。比如上例中\(\log^* 2^{65536} = 5\),因为 \(\log\log\log\log\log(2^{65536}) = 1\)
参考资料:阿克曼函数的详细介绍
An Application¶
应用:计算机网络中的文件传输(具体内容见课本 \(P_{279}\),也可以看看下面的编程题)
后续章节中会有更好的应用