Chap 6 Priority Queues(Heaps)¶
约 3322 个字 73 行代码 预计阅读时间 18 分钟
核心知识
- 二叉堆的表示:数组
- 常用操作:
Insert、DeleteMin,分别涉及“上滤”和“下滤“的思想 - 其他操作:
BuildHeap
何时用堆?
当我们只关心一个列表中最小(大)的元素时(频繁查找或使用),我们应优先使用堆
Simple Implementation¶
比较下列几种实现方式:
- 数组
- 插入:在尾部添加项 ~ \(\Theta(1)\)
- 删除:找最大/最小的键 ~ \(\Theta(n)\);删除项后移动剩余项 ~ \(O(n)\)
- 链表
- 插入:在头部添加项 ~ \(\Theta(1)\)
- 删除:找最大/最小的键 ~ \(\Theta(n)\);删除项 ~ \(\Theta(1)\)
- 有序数组
- 插入:找到正确的位置 ~ \(O(n)\);移动数组并加入该项 ~ \(O(n)\)
- 删除:移除首项/末项 ~ \(\Theta(1)\)
- 有序链表
- 插入:找到正确的位置 ~ \(O(n)\);加入项 ~ \(\Theta(1)\)
- 删除:移除首项/末项 ~ \(\Theta(1)\)
可以看出,这些结构实现起来相对比较容易,且各有优劣。一般情况下,插入的操作 > 删除的操作,因此教材作者更推荐链表。
What about BST(二分搜索树)?
二分搜索树有以下问题:
- 虽然理论上它的插入和删除操作时间复杂度为\(O(\log n)\),然而实际应用中插入操作是随机的,这会导致树的不平衡,从而影响时间复杂度
- 虽然删除操作并不是随机的,但我们只要找最小节点并且删除它,这会导致左子树越来越小,破坏了树的平衡,从而影响复杂度
- 我们可能想到构建一棵平衡的树,比如 AVL 树。但是 AVL 树中的很多操作在优先队列中用不到,且它的指针使用很危险。
ADT Model¶
优先队列/堆(priority queue/heap):
- Objects:含有 0 个或多个元素的有限有序表
- Operations:
PriorityQueue Initialize(int MaxElements);void Insert(ElementType X, PriorityQueue H);ElmentType DeleteMin(PriorityQueue H);ElementType FindMin(PriorityQueue H);
现在,我们正式介绍新的数据结构——二叉堆(binary heap, 简称堆(heap))
Binary Heap¶
Structure Property¶
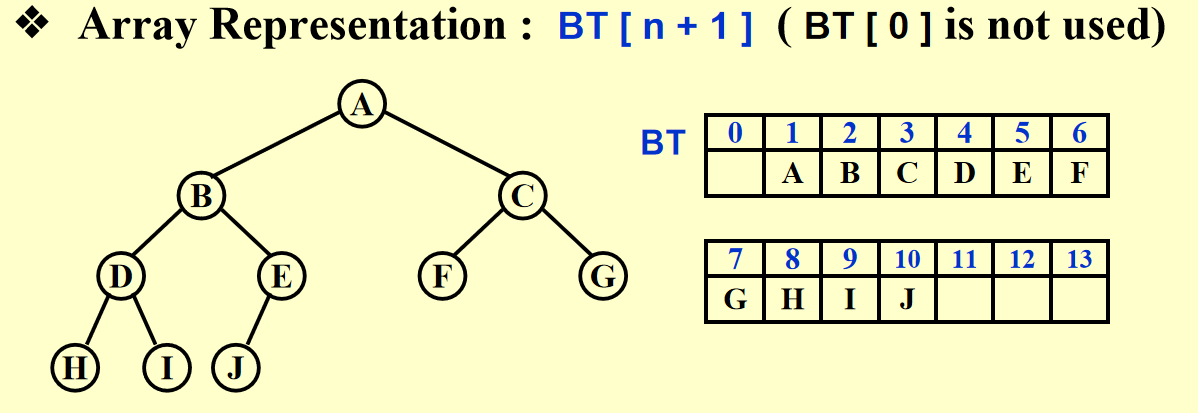
完全(complete)二叉树:一棵有 \(n\) 个节点且高为 \(h\) 的树,它的节点与一棵高为 \(h\) 的完美二叉树(perfect binary tree)的节点(从 1到 \(n\) 标号)一一对应
完美二叉树:除了最后一层外的所有节点都有两个孩子,最后一层的节点为叶子节点
另一种定义:除了最后一层外,每层的节点都填满,最后一层的节点从左往右填补的树
一棵高为 \(h\) 的完全二叉树有 \(2^h\)~\(2^{h + 1} - 1\) 个节点 \(\Leftrightarrow h = \lfloor \log N \rfloor\)
因为完全二叉树的规律性,我们可以使用数组存储二叉堆,用索引找到相应节点(见下面引理),十分简单,但创建堆的时候要考虑最大容量
🌟引理:如果一棵有\(n\)个节点的完全二叉树按层序表示,则对于索引为 \(i(1 \le i \le n)\) 的节点,我们有:
-
父节点的索引 \(= \begin{cases} \lfloor \dfrac{i}{2} \rfloor & \text{if } i \ne 1 \\ \text{None} & \text{if } i = 1\end{cases}\)
C语言的整数除法自动帮我们向下取整,因此直接除就行了
-
左孩子的索引 \(= \begin{cases} 2i & \text{if } 2i \le n \\ \text{None} & \text{if } 2i > n\end{cases}\)
-
右孩子的索引 \(= \begin{cases} 2i + 1 & \text{if } 2i + 1 \le n \\ \text{None} & \text{if } 2i + 1 > n\end{cases}\)
注
索引从 1 开始,看似只是为了得到比较舒服的表示法。但这样做后,索引为 0 的位置就空出来了,我们之后会利用这个位置,作为哨兵(sentinel)(将其设为整个堆的最小值),方便后面的插入和删除操作
声明部分:
struct HeapStruct
{
/* Maximum size that can fit in the heap */
unsigned int max_heap_size;
/* Current size of elements in the heap */
unsigned int size;
element_type *elements;
};
typedef struct HeapStruct *PriorityQueue;
Initialize¶
PriorityQueue Initiailize(int MaxElments)
{
PriorityQueue H;
if (MaxElements < MinPQSize)
return Error("Priority queue size is too small");
H = (PriorityQueue)malloc(sizeof(struct HeapStruct));
if (H == NULL)
return FatalError("Out of Space!!!");
// Allocate the array plus one extra for sentinel
H->Elements = (ElementType * )malloc((MaxElements + 1) * sizeof(ElementType));
if (H->Elements == NULL)
return FatalError("Out of Space!!!");
H->Capacity = MaxElements;
H->Size = 0;
H->Elements[0] = MinData; // set the sentinel
return H;
}
Heap Order Property¶
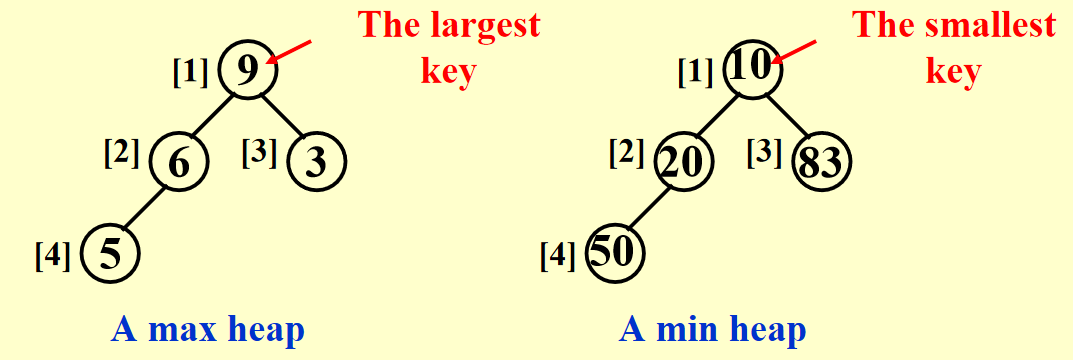
- 最小树(min tree):一棵树中每个节点的键值不大于它的孩子
- 最小堆(min heap):完全二叉树 + 最小树
我们也能以类似的方法定义最大堆,这里就不写出来了
- 显而易见,根节点是堆中最小(大)的节点
- 从堆的根节点出发,到任意节点的路径上的节点是有序的(比如最小堆中路径上的节点是按升序排列的)
- 但是对整个堆的遍历无法表示所有节点的顺序
Basic Heap Operations¶
Insertion¶
思路
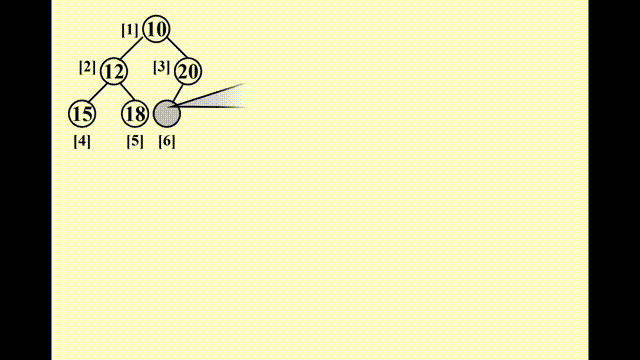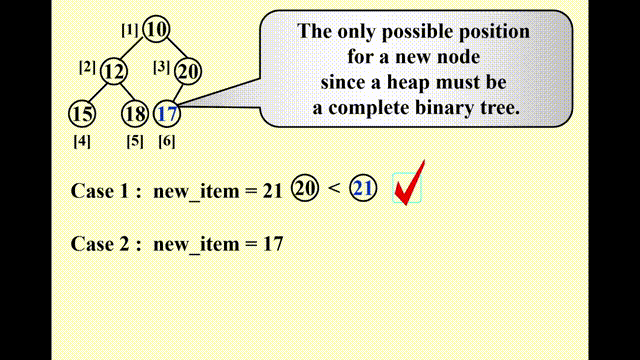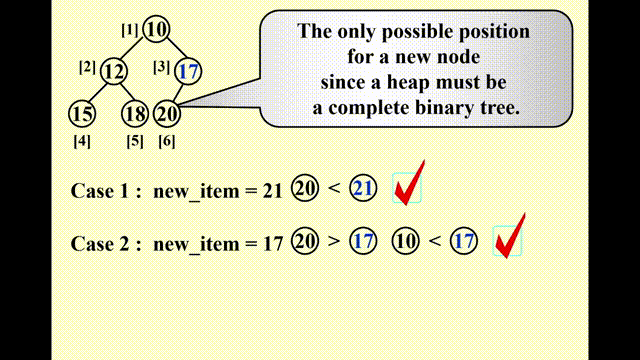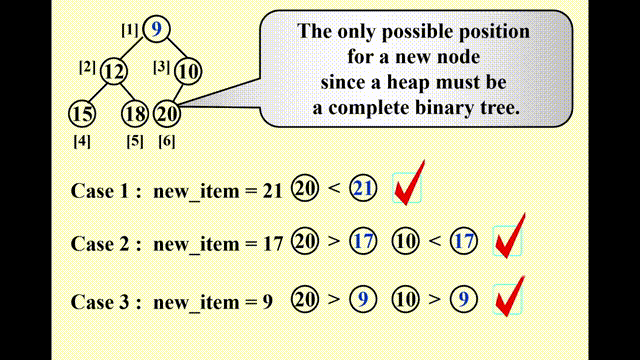
- 因为要保持完全二叉树的状态,因此唯一可插入节点的位置是最后一个位置
- 插入以后要调整节点的位置:
- 将该节点与其父节点比较,如果比父节点小,则将父节点往下移
- 重复该步骤,直至比当前比较的节点更大则停止,此时的位置即为新节点的位置
这种技巧被称为“上滤(percolate up)”。
代码实现
// H->Elements[0] is a sentinel
void Insert(ElementType X, PriorityQueue H)
{
int p = ++H->Size;
H->Element[p] = X;
PercolateUp(p, H);
}
void PercolateUp(int p, PriorityHeap H)
{
int i;
ElementType x = H->Elements[p];
for (i = p; H->Elements[i / 2] > x; i /= 2)
H->Elements[i] = H->Elements[i / 2];
H->Elements[i] = x;
}
- 在比较过程中,并没有直接交换两个数,因为实现一次交换就需要三条赋值语句。如果一个节点向上移动 \(d\) 层,则需要执行 \(3d\) 次运算;而上面的方法只需 \(d + 1\) 次运算,显然更快
- 正如上面所说,0 位置的节点被称为哨兵,将它的值设为整个堆的最小值。有了它,我们就不需要用“
while循环 + 根节点位置特判“这么麻烦,对待根节点也能像对待其他节点一样,因此只要用简单的for循环就能实现 - 时间复杂度:\(T(N) = O(\log N)\)
DeleteMin¶
思路
- 要找到最小值非常简单——就是首项
- 但是删除首项后,还是要保证该树是完全二叉树+最小树。因此实际上我们应删除最后一个节点,然后考虑如何安置原来在最后位置上的节点:
- 先将它放入根节点的位置(因为”删除“操作,这个位置空出来了),再让它和左右孩子比较
- 如果比左右孩子都大,则要将最小的孩子放入根节点
- 接着将它与这个孩子的左右孩子比较,……,直至比左右孩子都小为止
这种技巧被称为“下滤(percolate down)”。
代码实现
ElementType DeleteMin(PriorityQueue H)
{
ElementType MinElement;
MinElement = H->Elements[1];
H->Elements[1] = H->Elements[H->Size--];
PercolateDown(1, H);
return MinElement;
}
void PercolateDown(int p, PriorityQueue H)
{
int i, child;
ElementType last = H->Elements[p];
for (i = p; i * 2 <= H->Size; i = child)
{
child = i * 2;
if (child != H->Size && H->Elements[child + 1] < H->Elements[child])
child++;
if (last > H->Elements[child])
H->Elements[i] = H->Elements[child];
else
break;
}
H->Elements[i] = last;
}
- 看到
PercolateDown()函数的for循环中的第一个if语句:- 它考虑了只有一个左孩子的节点的情况
- 同时,它也选择了最小的孩子作为接下来的比较对象
- 可以使用另一个哨兵来移除这个
if语句:对于节点总数为偶数的堆(由完全二叉树的性质知,此时存在一个只有左孩子的节点),在最后位置的下一个位置上添加一个节点,并将其值设为整个堆的最大值,这样就可以防止某个节点下滤的时候被安置在不存在的节点上,而不需要特判 - 时间复杂度:\(T(N) = O(\log N)\)
Other Heap Operations¶
注意
- 如果我们想要频繁地查找某个列表中的任意元素,那么堆绝对不是合理的选择,因为在堆里找元素需要线性扫描(\(O(n)\))。我们应该采用二分搜索树、散列表等方法
- 在最小堆中找最大值也是不合理的,理由同上
\(\mathrm{DecreaseKey}(P, \Delta, H)\)
将位置为\(P\)的节点的键值减去 \(\Delta\),这样对应节点的优先级就会提高(上滤)
\(\mathrm{IncreaseKey}(P, \Delta, H)\)
将位置为\(P\)的节点的键值加上 \(\Delta\),这样对应节点的优先级就会下降(下滤)
注:这两个操作一般由系统管理员,而非一般的用户使用。比如:
- 前者可使某个程序提到最高优先级
- 后者可将占用CPU时间过多的进程的优先级往下调
\(\mathrm{Delete}(P, H)\)
从堆中移除位置为\(P\)的节点(删除由用户终止(非正常结束)的进程)。看似很复杂,实际上我们可以运用之前的 DecreaseKey() 和 DeleteMin() 函数,其中前者第二个参数令为 \(\infty\)(减去无限大的数,成为最小的数,然后利用 DeleteMin())
\(\mathrm{BuildHeap}(H)\)

方法
对于每个节点使用Insert()函数 \(\rightarrow O(N\log N)\) ?❌
采用“下滤”思想:
- 先将表中的元素按层序放入一棵完全二叉树中
- 然后从层序遍历中的最后一个内部节点开始,按层序的逆序到根节点为止,每个节点都需要使用
PercolateDown()函数,确定自己的最终位置
定理:对于一棵高为 \(h\),拥有 \(2^{h+1}-1\) 个节点的完美二叉树,所有节点高度之和为 \(2^{h+1} - 1 - (h+1)\)
由这个定理,可推得时间复杂度为:\(O(N)\)
代码实现:
for (i = N / 2; i > 0; i--)
PercolateDown(i);
Applications of Priority Queues¶
举例:
The Selection Problem¶
问题
给定\(N\)个元素,找到第\(k\)大的元素
算法
这两个算法易于理解但效率不高:
对所有元素排好序,再找第\(k\)大的数 \(\rightarrow O(N^2)\)
先取前\(k\)个数并对这些数排好序,再将剩余 \(N - k\) 个数分别与这 \(k\) 个数比较:如果比这 \(k\) 个数中最小的数更大,将最小的数踢出去,让待判断的数进去并放入正确的位置。
时间复杂度为 \(O(N \cdot k)\)。最坏情况 \(k = \lceil N/2 \rceil\) 时,时间复杂度为 \(O(N^2)\)
利用我们刚学的堆,可以得到两个复杂度均为 \(O(N \log N)\) 的算法:
为了方便起见,这里我们讨论找第 \(k\) 小的数(道理都是一样的)。先对这 \(N\) 个元素构建堆(使用 BuildHeap() 函数),然后使用 \(k\) 次 DeleteMin() 函数,最后一次从堆中得到的元素便是我们想要的第 \(k\) 小的元素。时间复杂度 \(O(N + k \log N)\),最坏情况为 \(k = \lceil N/2 \rceil\),时间复杂度为 \(\Theta(N \log N)\)
借鉴算法2的思想,先对前\(k\)个数构建堆(使用 BuildHeap() 函数),然后将剩下 \(N - k\) 个元素与堆中根节点(最小值)进行比较,如果比它大,则需要使用 DeleteMin() 和 Insert() 两个函数。时间复杂度为 \(O(k + (N - k)\log k) = O(N \log k)\),最坏情况为 \(\Theta(N \log N)\)
Event Simulation¶
问题
在银行中,顾客排在一列队伍中,等待 \(k\) 位出纳员中的一位有空。分析每位顾客的平均等待时间、队伍的长度
分析
该模拟中包含两个事件:顾客到达银行,顾客离开银行(一位出纳员因此处于空闲状态)
我们可以使用概率函数产生输入流,该输入流包含一组有到达时间和服务时间的有序对,按到达时间排序。我们不采用精确的时间,而是以 tick 作为计时单位。开始时,将 tick 初始化为 0;当没有顾客进来且所有出纳员都处于空闲状态时,模拟结束。
如果我们通过循环每个 tick 来处理整个程序的话,那么运行时间跟顾客和时间的数量无关,而且运行效率很低。因此我们根据最近时间发生的事件来增加 tick,这分为两种情况:下一位顾客的到来,有一位顾客离开。
对于正在排队的顾客,我们用队列来存储;对于每位顾客离开时间的存储,我们用优先队列存储,以便我们找到最近发生的事件。
时间复杂度:\(O(C \log(k + 1))\)
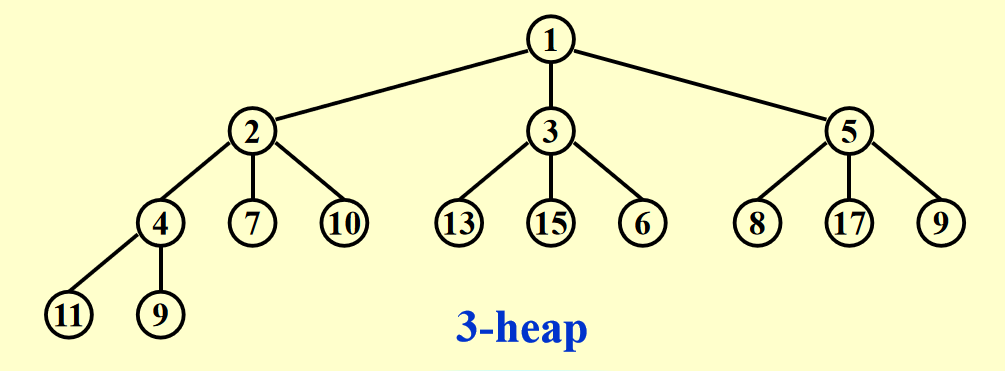
d-Heaps¶
d叉堆:所有节点最多有 \(d\) 个孩子
\(d\)并不是越大越好,理由如下:
- 虽然
Insert()速度变快(\(O(\log_dN)\)),但DeleteMin()要找到最小的孩子,需要 \(d - 1\) 次比较,因此时间复杂度将会变成 \(O(d \log_d N)\) - 在找某个节点的左右孩子或父节点时,二叉堆中的 \(\times 2\) 或 /2 仅仅是个移位操作,但d-Heap中的 \(\times d\) 或 \(/ d\) 则更加复杂
优势:
- 就如前文所说,插入操作往往比删除操作多,因此我们从
Insert()的提速中获得的好处比DeleteMin()的降速带来的弊端更多 - 如果优先队列太大,以至于主内存无法容纳,则d-Heap比二叉堆更有优势
补充:对于节点\(i\)
- 父节点:\(\lfloor \dfrac{i + d - 2}{d} \rfloor\)
- 第一个孩子:\((i - 1)d + 2\)
- 最后一个孩子:\(id + 1\)